Radix Sort in C

Radix Sort is a non-comparative sorting algorithm that sorts numbers by processing individual digits. It is a linear time complexity algorithm that is used to sort numbers in a fixed range. The algorithm works by sorting numbers based on their individual digits, starting from the least significant digit to the most significant digit.

Radix Sort typically uses Counting Sort as a subroutine to sort numbers based on each digit. Counting Sort efficiently sorts numbers in a specific range, making it well-suited for digit-based sorting in Radix Sort.

When I was implementing Radix Sort in C, I did not use Counting Sort as a subroutine. Instead, I implemented the algorithm using Linked Lists to store numbers in each bucket. This approach is less efficient than using Counting Sort, but it is easier to understand and implement.

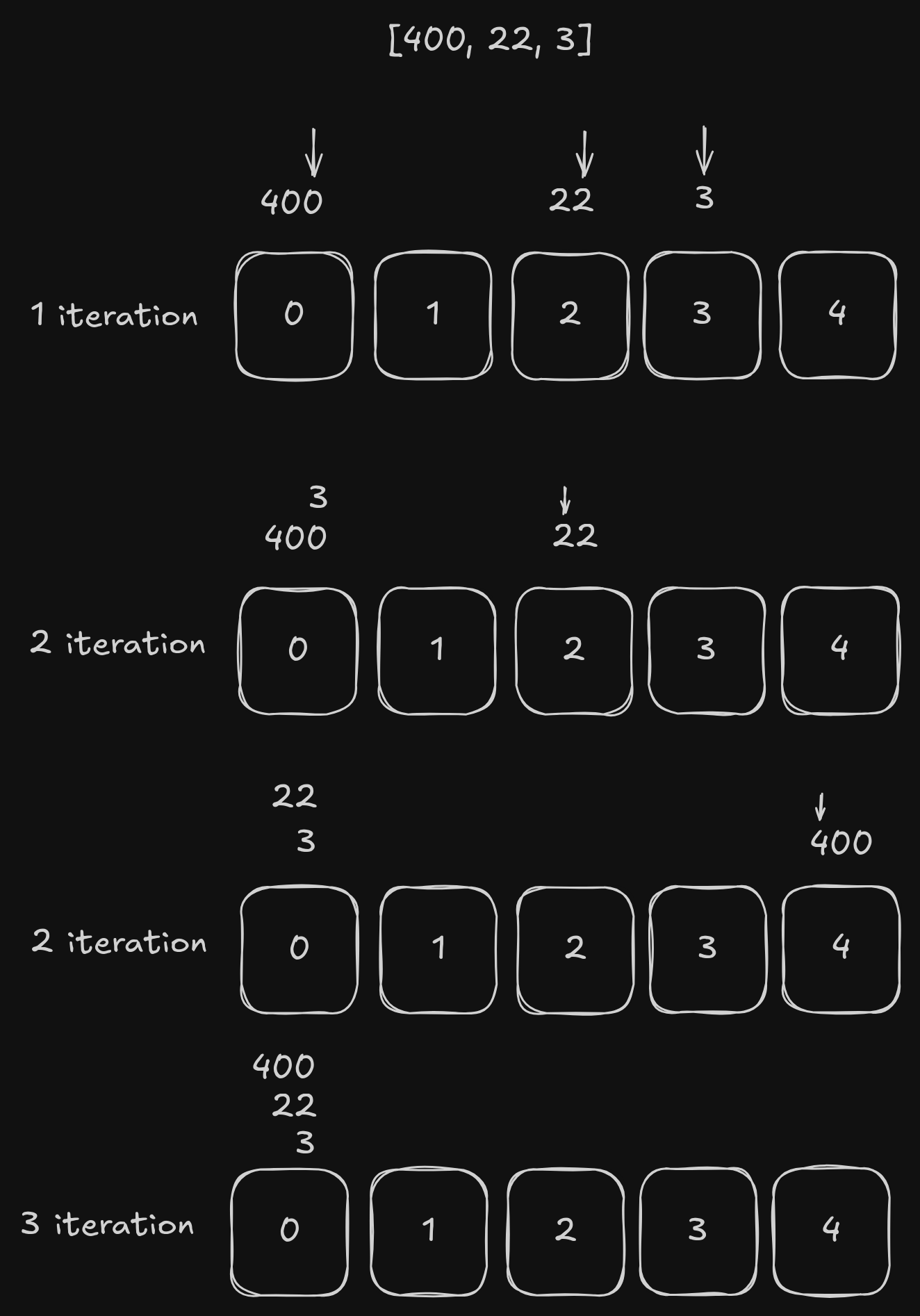
In short, in order to sort the array, we are creating 10 (0-9) buckets and storing the numbers in the respective bucket based on the digit at the current position. Then, we are incrementing the offset and repeating the process until the array is sorted.

Pre-requisites

Before trying to implement Radix Sort, you should be familiar with it’s concepts and how it works. You should also have a good understanding of Linked Lists and how to implement them in C.

• Radix Sort
• Linked Lists
• Linked Lists in C
• Counting Sort

Implementation

First, let’s create the Linked List structure to store numbers in each bucket:

struct node {
    int data;
    struct node* next;
};

Next, we need to implement the function to find the last node in the Linked List:

// @param bucket: single Linked List
struct node *findLast(struct node *bucket) {
    if (!bucket) return NULL;
 
    while (bucket->next) {
        bucket = bucket->next;
    }
    return bucket;
}

Next, we need to implement the function to insert a number into the Linked List:

// @param buckets: array of Linked Lists
// @param bucket: index of the bucket
// @param value: number to insert
void push(struct node *buckets[], int bucket, int value) {
    struct node *new = malloc(sizeof(struct node));
    if (!new)
        return;
    
    new->data = value;
    new->next = NULL;
 
    if (!buckets[bucket]) {  
        // set as head if the list is empty
        buckets[bucket] = new;
    } else {
        // otherwise, attach to the end of the list
        struct node *last = findLast(buckets[bucket]);
        last->next = new;
    }
}

The push function inserts a number into the Linked List at the specified bucket. If the bucket is empty, the number is set as the head of the Linked List. Otherwise, the number is inserted at the end of the Linked List.

Few more supporting functions are required to complete the implementation:

• find_largest: Find the largest number in the array and return it.
• count_digits: Count the number of digits in a number.
• get_digit_offset: Get the digit at the specified offset in a number. Returns zero if the offset is greater than the number of digits in the number.
• free_buckets: Free the memory allocated for all the Linked Lists.

// @param arr: array of numbers
// @param size: size of the array
int find_largest(int *arr, size_t size) {
    int result = arr[0];
    int i = 1;
    while (i < size) {
        if (result < arr[i]) {
            result = arr[i];
        }
        i++;
    }
    return(result);
}

// @param num: number
int count_digits(int num) {
    int result = 1;
    while (num > 0) {
        num /= 10;
        result++;
    }
    return result;
}

// @param num: number
// @param offset: digit offset
int get_digit_offset(int num, int offset) {
    if (offset == 0)
        return num % 10;
    
    int result = num;
    while (offset--) {
        result /= 10;
    }
    return result % 10;
}

Great. Finally, we can implement the Radix Sort function:

void radix_sort(int *arr, size_t arr_size) {
    if (!arr_size || arr_size == 1) {
        return;
    }
    int largest = find_largest(arr, arr_size);
    int largest_digits_count = count_digits(largest);
    int sorted_count = 0;
 
    // max amount of digits in the largest number equals to the amount of times we need to loop
    while (largest_digits_count > sorted_count) {
        struct node *buckets[10] = {NULL};
        int i = 0;
 
        // loop through each digit and push to respective bucket
        while (i < arr_size) {
            int bucket_digit = get_digit_offset(arr[i], sorted_count);
            push(buckets, bucket_digit, arr[i]); 
            i++;           
        }
        
        // after setting buckets, go through each sub-bucket and assign sorted values directly to *arr
        i = 0;
        for (int j = 0; j < 10; j++) {
            struct node *curr = buckets[j];
            while (curr) {
                arr[i++] = curr->data;
                curr = curr->next;
            }
        }
        
        // free all buckets
        free_buckets(buckets);
        sorted_count++;
    }
}

If we were to add some logging, we could see how the algorithm sorts the array:

void print_bucket(struct node *bucket) {
    if (!bucket) {
        return;
    }
 
    struct node *curr = bucket;
    while (curr) {
        printf("%d -> ", curr->data);
        curr = curr->next;
    }
    printf("NULL\n");
}
 
void print_all_buckets(struct node *buckets[]) {
    int i = 0;
    while (i < 10) {
        print_bucket(buckets[i]);
        i++;
    }
}

devnyxie:push_swap$ ./a.out
=== iteration 0 === 
400 -> NULL
22 -> NULL
3 -> NULL
=== iteration 1 === 
400 -> 3 -> NULL
22 -> NULL
=== iteration 2 === 
3 -> 22 -> NULL
400 -> NULL
=== iteration 3 === 
3 -> 22 -> 400 -> NULL
3 22 400

Conclusion

I really hope you enjoyed this article and learned something new. Radix Sort is a fascinating algorithm, really. It’s a great example of how we can sort numbers in linear time complexity by processing individual digits.