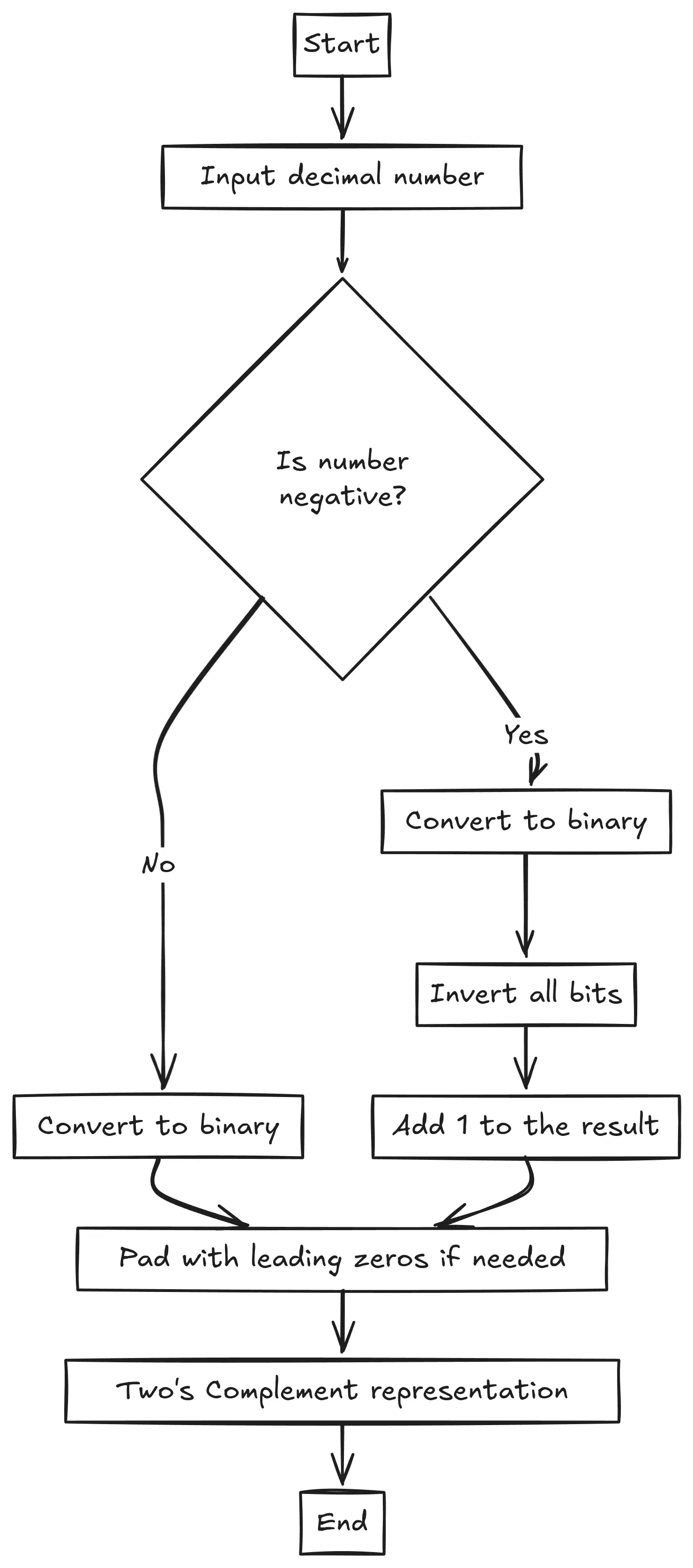
Two's Complement Form

Two’s complement is a way of representing signed integers in binary. Here’s how it differs from the standard binary representation in C:

---

Binary Representation

• Binary is the raw representation of numbers using 0s and 1s.
• Unsigned binary represents only non-negative numbers (0 and positive numbers).

For example:

• Decimal 5 → 00000101 (8-bit binary)
• Decimal 12 → 00001100 (8-bit binary)

This representation doesn’t handle negative numbers.

---

Two’s Complement Representation

• Two’s complement is used for signed integers, which can represent both positive and negative numbers.
• **Key differences:
  1. The most significant bit (MSB) becomes the sign bit:
     • 0 = Positive
     • 1 = Negative
  2. Negative numbers are encoded by taking the two’s complement of their absolute value:
     • Invert all bits (~n)
     • Add 1 to the result.

For example, in 8-bit representation:

• Decimal 5 → 00000101 (same as binary, MSB is 0)
• Decimal -5:
  • Start with 5 → 00000101
  • Invert bits → 11111010
  • Add 1 → 11111011

Thus, -5 is represented as 11111011.

---

Practical Differences in C

Unsigned (Binary Representation)

• unsigned int is always treated as a positive number.

  unsigned int x = 250;  // 250 is stored as binary directly

Signed (Two’s Complement Representation)

• int (signed by default) uses two’s complement to represent negative numbers.

  int y = -5;  // Stored as 11111011 in two's complement

Key Behaviors

• Arithmetic:
  • Two’s complement enables seamless addition/subtraction of positive and negative numbers without requiring special handling.
• Overflow:
  • For signed integers, exceeding the range (e.g., adding to INT_MAX) causes wraparound in two’s complement. More on Integer Overflow.

---

Example in Code:

#include <stdio.h>
 
int main() {
    int a = 5;         // Positive number, binary: 00000101
    int b = -5;        // Negative number, two's complement: 11111011
    unsigned int c = 5; // Binary representation: 00000101
    return 0;
}

---

In summary:

• Binary representation is straightforward and used for unsigned integers.
• Two’s complement is the standard for signed integers because it simplifies arithmetic operations with mixed positive and negative numbers.